A Personal Message From the CEO of John Boom Tutoring:
Dear Loyal Readers,
Previously, on other blogs of mine you may have read, that I went to great trouble chasing away the ferocious ad beasts. However, since this is my business page and not my personal page, I do not in the least feel that I have "sold out" by allowing ads here, for that is this page's purpose--to make money. Hopeful readers fear not, for I still staunchly defend my other blog-homes keeping them safe from whiles of the ad-paparazzi, but while they may, ads may safely rest here. Be aware though, I do not endorse, nor agree with, nor even necessarily know anything about what is being sold here. Click at your own discretion. I will try to keep it family appropriate and minimally annoying. It is after all, my blog too.
Sincerely,
John Boom-CEO and Owner John Boom Tutoring
P.S Send me your feedback. Let me know what you think. If there is something you are struggling with post a comment somewhere and I will put up a reply. Best of luck! Hope all is well. Cheers to you.
Our mission is to EMPOWER and EMPASSION students and future-professionals in the fields of biology, chemistry, physics & math.
Monday, March 26, 2012
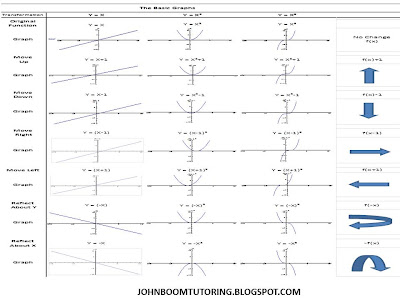
All Possible Graphs
Variations on Common Inverse Trig-Integrations
The following are variations of the common Inverse Trigonometric Integrals starting with ArcTan, moving to ArcSec, and concluding with the ArcSin.
Solving
things like the integrals above is
relatively "easy" Once you pick up the pattern. They usually require only
applications of the Pythagorean identity and some creative algebra. That is…
A2
+ B2 = C2 or in trig speak…
Sinθ2
+ Cosθ2 = 1
Which
if we divide both sides by Cosθ2 can be rearranged as
Tanθ2
+ 1 = Secθ2
Thus
giving us the three identities we need to solve the above problems.
x2
+ 1 = Tanθ2 + 1 = Secθ2
x2
– 1 = Secθ2 -1 = Tanθ2
1-x2
= 1- Sinθ2 = Cosθ2
Thus
if we see x2 +1 we want to set x = Tanθ with the associated
implications that θ = Tan-1 x and dx = sec2θ. We do this because if x = Tanθ we can totally
rock the identity we derived that Tanθ2 + 1 = Secθ2. Similarly if we see things of the form x2
– 1 we will want to let x = Secθ with dx = Secθ Tanθ dθ. And finally, if you see 1-x2 let x = Sinθ and let dx = Cosθ. The use of trig identities was, after all, the entire reason we
made the wacky substations in the first place was so we could get some trig
identity action working in our favor.
Making these substitutions leaves us with…
( ___dx___
= ( __ sec2θ dθ =
( dθ = θ + C = ArcTan x +C or Tan-1x
+ C
) x2 + 1 ) sec2θ )
Sweet,
letting x = Tanθ was a pretty good idea, especially when combined with that
trig identity we tossed in there canceling the Secθ2 ! NOTE: letting X = Tanθ also works if I have 1+X2 because A+B is the same as B+
A.
This next one though it looks simple is a bit
messier. But let’s dive in.
( ___dx___
) x2 – 1
This
time let X = Secθ. If we do this I can
get this to simplify using Secθ2 -1 = Tanθ2. If x = Secθ this means θ = Sec-1x. It also means that dx = d(Secθ). I always remember the derivative of secant with the phrase "dseek tan destroy" playing off of the phrase seek and destroy representing the answer to the derivative of secant = SecθTanθ dθ. Making these
switches leaves us…
( ___dx___ = ( __ SecθTanθ dθ ___= (
__ SecθTanθ dθ ___= ( __
Secθ dθ_ =(__1/Cosθ__dθ
) x2 – 1 ) Secθ2 -1 ) Tanθ2 ) Tanθ )
Sinθ/Cosθ =
(
__ 1/Sinθ dθ__ = ( CSCθ dθ
) ) =Eew Gross!-- use a table, or magically pull out of your butt the trick
of timesing
by __ Cscθ +Cotθ___
Cscθ + Cotθ
and using a U substitution where U = the denominator an dU = the numerator. Where the Heck did that come from? Don’t worry about it, use a table. Anyway
when the dust settles integral solves to
= - ln |csc x + cot x| + C
Solution Courtesy of http://www.math.com/tables/integrals/more/csc.htm
Note: It might also be easier to solve Integral
with partial fractions.
I
can also use the general strategy of letting x = Secθ to solve the more
complicated looking integral:
(___ dx____
)
x √(x2 -1)
Again
let x = Secθ, Sec-1(x) = θ and dx =
SecθTanθdθ. Making the appropriate substitutions leaves.
(___SecθTanθdθ ____ Using the identity = Secθ2 -1 = Tanθ2
) Secθ
√( Secθ 2 -1)
(___SecθTanθdθ
_ = (_SecθTanθdθ _ = ∫dθ = θ + C = Sec-1 (x) +C
) Secθ
√( Tanθ2) ) SecθTanθdθ
Finally,
let’s explore
( ___dx___
This one looks most similar in form to the Sin2θ identity so
let x = Sinθ
)
1-x2
If
X = Sinθ then θ = Sin-1(x) and dx = Cosθ dθ replacing.
(__
Cosθ dθ_ The bottom has an identity
I can use to simplify. 1 – Sin2θ
= Cos2 θ. Let’s use it.
)
1-Sinθ2
(__
Cosθ dθ_ = (__ Cosθ dθ_
= ( __dθ__ = ∫ Secθ dθ =
crud! I have to do more magic tricks.
) 1-Sinθ2 ) Cosθ2 )
Cosθ
In
this case, the magic trick I need to do is times by ___Secθ +Tanθ___
Secθ + Tanθ
Where did
that come from? The same bag
of fairy dust that let me solve the Cscθ integral we ran into earlier. Any way, this integral is evaluated by letting U equaling the new
bottom U = Secθ + Tanθ and du = Secθ Tanθ + Sec2 θ my old integral
turns into the new and improved version
∫
du/u = Ln| Secθ + Tan θ | + C Where θ = Sin-1 (x) which leaves us
the nasty looking
Ln|
Sec(Sin-1 (x) ) + Tan (Sin-1 (x) ) | + C.
We can draw a trangle and get it a bit more
solved and nicer looking, but hey our teacher has a Ph.D in math we’ll let him
do the algebra if he wants it. For our
purposes we are done. But that integral
looked horrible so let’s examine a variation of the previous one.
If instead our integral
looked like…
(___ dx____ We could make the same
substitution as before let x = Sinθ
)
√(1-x2 )
Thus
θ = Sin_1(x) and dx = Cosθ dθ. The identity 1 – Sinθ2 =
Cosθ2 applies And Voila…
(
__ Cosθ dθ__ = ∫dθ =θ + C = Sin-1 (x) +C
)
Cosθ
Ah
good now that we know
a.
( (___dx___
= ArcTanx + C
) x2 + 1
(___ dx____ = ArcSec x +C
) x √(x2 -1)
And (___ dx____ = ArcSin x +C
) √(1-x2 )
By similar logic we arrived at the variations above. As a final NOTE: It is useful to remember the identity Cosθ2 =(1/2)[ 1+ Cos(2θ)]. This is a great way of drooping a squared exponent to a more manageable linear cos term.
Stoichiometry: Aka Units of Doom!
Greetings all, I have decided to post my explanations to common questions I am asked about math, chemistry, physics and biology. Today's post is about stoichiometry in other words, unit conversions. This is single-handedly THE most important topic in all of chemistry. If you can master unit conversions you have 3/4ths of chemistry and 1/3 of physics down.
Here are some questions to get your brain juices thinking. The answers to these questions should clear up your questions. It may seem a little out in left field but stay with me.
What is 3/3? How about 12/12? 127/127? 435296/435296?
The answer to all of them is 1.
Now what is 1*3? How about 1*5? 1* 437?
Does timesing by 1 change the number you are multiplying by?
No. One is what is called the multiplicative identity. Meaning I can times anything by one and it doesn't change the number, only what it looks like. 1*5 looks a little different than just 5 but it still = 5. This is useful for chemistry because I can change the units of the quantity I am working with without changing the amount. By doing unit conversions I am really multiplying by a complicated version of the number one (The loneliest number).
Next question, am I the same person if I stand on my head? Am I the same if I lie on my side? In short does it matter what orientation I am in or am I still me even on my head?
Of course I am the same. The same is true for conversion factors. They still work even if they are upside down.
A few more things then we will get to the actual chemistry.
___________|_____________|____
| | |
This is what I like to call "railroad tracks." Its a table that I will use to keep track of what units I am in an what units I am converting into. This is one of the most important tables in all of chemistry (the other is the periodic table.) This little table lets me know instantly if I got a problem right or not. This is one reason I love chemistry it is one of the few things with instant feedback for a correct response to a tricky puzzle. If you can master this table you have most of chemistry mastered. For at least the first 2.5 years of chemistry all it really is is a series of fancy unit conversions.
Lets practice one problem using this table to make sure we get the hang of it (Note this table can be as long or as short as I need it depending on the problem.). Suppose you are given the problem, "How many seconds are in 45 years?" How on Earth do you begin? Simple. Search the problem for a number that has only 1 unit attached to it. In this case ___ years. Years is only one unit If I had something like Kg m/s^2 that is four units all lumped together, one usually doesn't start with that. There are some exceptions where it is actually easier to start with the messiest looking thing, but usually start with the given that has one unit. In this case years. The thing you are starting with goes in the top left square of our rail road tracks.
__45 years_|_____________|_________
| | |
What is a conversion factor you know involving years?
Oh I know ~365 days/year.
Ok so where do I put it? Well I want my years to cancel so it must go on the bottom.
__45 years_|_365 days___|____________|_________
| 1 years | |
Note: "per" means put it on the bottom. Miles PER hour = __miles__
If I did this WRONG my units would not cancel. It would look like...
__45 years_|_1 years______|____________|_____
| 365 days | |
And I would be left with units of Years ^2/day. And I ask you, what the heck is a square year per day!? What does that even mean. Seeing the above I would immediately recognize Ooops ! I did something wrong. Seeing this its a simple fix to erase the part that is wrong and flip it over. In fact if i can't think of anything else to do start converting units stop when the units are what I want. If you don't get full credit for this you will at least get quite a bit of partial credit. So lets continue. What is a conversion factor involving days? 24 hours/day. Plug in appropriately and you get...
__45 years_|_365 days___|___24 hours_____|_________
| 1 years | 1 day |
Continue with 60s= 1 min and 60 min = 1 hr. And your final table looks something like this...
_45 years_|_365 days___|___24 hours_____|___60 min__|_60 sec___
| 1 years | 1 day | 1 hr | 1 min
Aha! I am not in units of secconds, the units I wanted. To make sure I did every thing right, I double check to make sure all of the others canceled. Years divided by years, days divided by days, hours/hr & min/min. Sure enough they all canceled. I am left with seconds, which is the units I wanted all along. Ok great! Now what? What do I do with this table. Times everything that is on top by each other (just the numbers I already got rid of the units.) And divide by everything on the bottom. When I enter this into my calculator I should enter it as follows:
"(45*365*24*60*60) / (1*1*1*1) = "
Note: The parenthesis are VERY VERY important. In our case the bottom was just 1*1 and we can do that in our head. However, you are not always so lucky to have ones on the bottom. Sometimes you will have numbers like 6.022*10^23 or other giant beasts lurking in your basement. If you do not put parenthesis your calculator will take one number divide it by another and then multiply it by your bottom. I actually saw someone make this mistake.
__3 Units A__|__ 5 Unit B___|__ 1 Unit C__
| 2 Units A | 6.022*10^23 Units B
He entered it into his calculator as:
3*5*1 / 2*6.022*10^23
The calculator interpreted this as...
3*5*1*6.022*10^23 / 2
So because he didn't use parenthesis my tutee was off by 45 orders of magnitude!
How he should have entered it is like so...
"(3*5*1) / (2*6.022*10^23)"
That way the calculator will divide by 1.2044*10^24 instead of dividing by 2. Big difference! USE parenthesis!
Now to the questions at hand (From this point forward you will need a periodic table--go get one!)
1) Determine the mass of Sodium hydroxide produced when (whenever you see a decimal point put a 0 in front of it, it is harder to loose track of 0.~~ than .~~. You are less likely to think it is a random pencil squiggle than a decimal point if you include the 0. So always include a 0) 0.47 g of Sodium nitride reacts with water according to the following equation: Na(3)N + 3H(2)O ---- NH(3) + 3NaOH
Step 1. Set up the railroad tracks.
___________|_____________|____
| | |
Step 2. Find what is given with only 1 unit.
0.47g NA(3)N Include the name of what you are playing with. It is quite common in chemistry to go from moles of A to moles of B so include the As and Bs to avoid getting lost.
Step 3. Fill in the table.
___0.47 g Na3N___|_____________|________
| | |
How much does 1 mole of Na3N weigh? Pull out your periodic table look at the numbers on the bottom add them together i.e. 3*23.99 for the 3 sodiums +14.01 for the Nitrogen for a total weight of 85.98 amu, but what the heck is an AMU? Is it some sort of guns store? No it stands for grams/mole. Hey we have grams on our chart lets plug in the weight and convert it to moles. But where does it go, on top or on the bottom? Where must we put it so that grams will cancel? On the bottom of course.
___0.47 g Na3N___|____1 mole_Na3N__ |____________|_________
| 85.98 g | |
Now where do I find the ratio of sodium nitride to sodium hydroxide? If only there was something that told me how much Na3N and NaOH would react together. If only I had some sort of equation relating all my reactants and products telling me how much of each I would need. If only I had such an equation I would be set. Oh I do have such an equation. For every 1 mole of Na3N I produce 3 moles of NaOH. Incidently the numbers of the balanced reaction coefficients work for volumes and numbers of atoms but not for mass. Consider this: I weigh 200 pounds. In this room right now there are 600 pounds. Does this mean there are three of me? No. So balanced reactions do not work for mass, only volumes and number of atoms.
___0.47 g Na3N___|____1 mole_Na3N__ |___3 mole NaOH__|_40 g________
| 85.98 g | 1 mole Na3N | 1 mole NaOH
Final step find the mass of sodium hydroxide. 23+16+1.
Times it out and you get...
(0.47*1*3*40)/(85.98*1*1) = your answer. Don't forget the parenthesis!
For Mass-mass use the periodic table. For mass-volume conversions you will need to use the density (mass/volume) or the concentration (moles/liter). For Volume-Volume use the coefficients of the balanced reaction (or possibly the ideal gas law if it is a gas.).
For limiting reactants you have to actually do the problem 2x. Once assuming one of the reagents is the limiting and again assuming the other is the limitant. The trick is to start with a balanced reaction and to pick one substance and convert everything into that one substance. So for example 2. I would set it up as follows...
1. Balance the reaction
__O2 +__H2 = __H2O
When I do this I get...
1-O2 + 2-H2 = 2-H2O
2. Plug in numbers
___2.41 g O2__(From Question)_|_1 mole O2 (From Reaction)_______ |_2 mole H2O (From Rxn)
| 32.00 g O2 (From Periodic Table) | 2 mole H2
= A moles of Water
___3.67 g H2___|____1 mole H2___ |___2 moles H2O__ = B moles Water
| 2.02 g H2 | 2 mole H2
Compare A and B see which one is smaller. The one that ones out first is the limiting reactant. So if A is smaller than B. Oxygen must run out first and therefore oxygen would be the limiting reactant.
% yield is just how much I got divided by how much I should have got *100 to make it a percent.
Usually they will give you how much you actually got and how much you started with. Use the amount you started with to calculuate how much you should have had if you did it perfectly.
Consider the reaction
C + 2-H2 explodes and makes CH4. I put explodes because it sounded cooler. It doesn't really.
Suppose you started with 3.0 g H and you produced 2.7 grams C what is your % yield.
If I did this perfectly all of H should react to produce CH4. Using a periodic table I find H2 weighs 2.02 g/mole. While CH4 weighs 16.05 g/mole.
___3.0 g H2___|_1 mole H2___ |___1 mole CH4 _|_ 16.05 g____| = 11.9 g CH4
| 2.02 g H2 | 2moles H2 | 1 mole CH4 |
Wait how can my theoretical mass be larger than the mass of hydrogen I started with? I added carbon as well. Oh yea. Though my final mass should never be larger that the sum of both parts I added. Carbon AND Hydrogen. If it is I did something wrong.
So If I did it perfect i should haved produced 11.9 g CH4 I actually produced 2.7g.
%Yield = actual yield / Theoretical Yield or real world/ perfect world
=> (2.7 / 11.9)*100 = 22.9% Yea! My reaction lost 87.1% of the stuff I put into it. Meaning I spilled most of my beaker. If my percent yield is ever greater than 100% I probably did something wrong.
Here are some questions to get your brain juices thinking. The answers to these questions should clear up your questions. It may seem a little out in left field but stay with me.
What is 3/3? How about 12/12? 127/127? 435296/435296?
The answer to all of them is 1.
Now what is 1*3? How about 1*5? 1* 437?
Does timesing by 1 change the number you are multiplying by?
No. One is what is called the multiplicative identity. Meaning I can times anything by one and it doesn't change the number, only what it looks like. 1*5 looks a little different than just 5 but it still = 5. This is useful for chemistry because I can change the units of the quantity I am working with without changing the amount. By doing unit conversions I am really multiplying by a complicated version of the number one (The loneliest number).
Next question, am I the same person if I stand on my head? Am I the same if I lie on my side? In short does it matter what orientation I am in or am I still me even on my head?
Of course I am the same. The same is true for conversion factors. They still work even if they are upside down.
A few more things then we will get to the actual chemistry.
___________|_____________|____
| | |
This is what I like to call "railroad tracks." Its a table that I will use to keep track of what units I am in an what units I am converting into. This is one of the most important tables in all of chemistry (the other is the periodic table.) This little table lets me know instantly if I got a problem right or not. This is one reason I love chemistry it is one of the few things with instant feedback for a correct response to a tricky puzzle. If you can master this table you have most of chemistry mastered. For at least the first 2.5 years of chemistry all it really is is a series of fancy unit conversions.
Lets practice one problem using this table to make sure we get the hang of it (Note this table can be as long or as short as I need it depending on the problem.). Suppose you are given the problem, "How many seconds are in 45 years?" How on Earth do you begin? Simple. Search the problem for a number that has only 1 unit attached to it. In this case ___ years. Years is only one unit If I had something like Kg m/s^2 that is four units all lumped together, one usually doesn't start with that. There are some exceptions where it is actually easier to start with the messiest looking thing, but usually start with the given that has one unit. In this case years. The thing you are starting with goes in the top left square of our rail road tracks.
__45 years_|_____________|_________
| | |
What is a conversion factor you know involving years?
Oh I know ~365 days/year.
Ok so where do I put it? Well I want my years to cancel so it must go on the bottom.
__45 years_|_365 days___|____________|_________
| 1 years | |
Note: "per" means put it on the bottom. Miles PER hour = __miles__
If I did this WRONG my units would not cancel. It would look like...
__45 years_|_1 years______|____________|_____
| 365 days | |
And I would be left with units of Years ^2/day. And I ask you, what the heck is a square year per day!? What does that even mean. Seeing the above I would immediately recognize Ooops ! I did something wrong. Seeing this its a simple fix to erase the part that is wrong and flip it over. In fact if i can't think of anything else to do start converting units stop when the units are what I want. If you don't get full credit for this you will at least get quite a bit of partial credit. So lets continue. What is a conversion factor involving days? 24 hours/day. Plug in appropriately and you get...
__45 years_|_365 days___|___24 hours_____|_________
| 1 years | 1 day |
Continue with 60s= 1 min and 60 min = 1 hr. And your final table looks something like this...
_45 years_|_365 days___|___24 hours_____|___60 min__|_60 sec___
| 1 years | 1 day | 1 hr | 1 min
Aha! I am not in units of secconds, the units I wanted. To make sure I did every thing right, I double check to make sure all of the others canceled. Years divided by years, days divided by days, hours/hr & min/min. Sure enough they all canceled. I am left with seconds, which is the units I wanted all along. Ok great! Now what? What do I do with this table. Times everything that is on top by each other (just the numbers I already got rid of the units.) And divide by everything on the bottom. When I enter this into my calculator I should enter it as follows:
"(45*365*24*60*60) / (1*1*1*1) = "
Note: The parenthesis are VERY VERY important. In our case the bottom was just 1*1 and we can do that in our head. However, you are not always so lucky to have ones on the bottom. Sometimes you will have numbers like 6.022*10^23 or other giant beasts lurking in your basement. If you do not put parenthesis your calculator will take one number divide it by another and then multiply it by your bottom. I actually saw someone make this mistake.
__3 Units A__|__ 5 Unit B___|__ 1 Unit C__
| 2 Units A | 6.022*10^23 Units B
He entered it into his calculator as:
3*5*1 / 2*6.022*10^23
The calculator interpreted this as...
3*5*1*6.022*10^23 / 2
So because he didn't use parenthesis my tutee was off by 45 orders of magnitude!
How he should have entered it is like so...
"(3*5*1) / (2*6.022*10^23)"
That way the calculator will divide by 1.2044*10^24 instead of dividing by 2. Big difference! USE parenthesis!
Now to the questions at hand (From this point forward you will need a periodic table--go get one!)
1) Determine the mass of Sodium hydroxide produced when (whenever you see a decimal point put a 0 in front of it, it is harder to loose track of 0.~~ than .~~. You are less likely to think it is a random pencil squiggle than a decimal point if you include the 0. So always include a 0) 0.47 g of Sodium nitride reacts with water according to the following equation: Na(3)N + 3H(2)O ---- NH(3) + 3NaOH
Step 1. Set up the railroad tracks.
___________|_____________|____
| | |
Step 2. Find what is given with only 1 unit.
0.47g NA(3)N Include the name of what you are playing with. It is quite common in chemistry to go from moles of A to moles of B so include the As and Bs to avoid getting lost.
Step 3. Fill in the table.
___0.47 g Na3N___|_____________|________
| | |
How much does 1 mole of Na3N weigh? Pull out your periodic table look at the numbers on the bottom add them together i.e. 3*23.99 for the 3 sodiums +14.01 for the Nitrogen for a total weight of 85.98 amu, but what the heck is an AMU? Is it some sort of guns store? No it stands for grams/mole. Hey we have grams on our chart lets plug in the weight and convert it to moles. But where does it go, on top or on the bottom? Where must we put it so that grams will cancel? On the bottom of course.
___0.47 g Na3N___|____1 mole_Na3N__ |____________|_________
| 85.98 g | |
Now where do I find the ratio of sodium nitride to sodium hydroxide? If only there was something that told me how much Na3N and NaOH would react together. If only I had some sort of equation relating all my reactants and products telling me how much of each I would need. If only I had such an equation I would be set. Oh I do have such an equation. For every 1 mole of Na3N I produce 3 moles of NaOH. Incidently the numbers of the balanced reaction coefficients work for volumes and numbers of atoms but not for mass. Consider this: I weigh 200 pounds. In this room right now there are 600 pounds. Does this mean there are three of me? No. So balanced reactions do not work for mass, only volumes and number of atoms.
___0.47 g Na3N___|____1 mole_Na3N__ |___3 mole NaOH__|_40 g________
| 85.98 g | 1 mole Na3N | 1 mole NaOH
Final step find the mass of sodium hydroxide. 23+16+1.
Times it out and you get...
(0.47*1*3*40)/(85.98*1*1) = your answer. Don't forget the parenthesis!
For Mass-mass use the periodic table. For mass-volume conversions you will need to use the density (mass/volume) or the concentration (moles/liter). For Volume-Volume use the coefficients of the balanced reaction (or possibly the ideal gas law if it is a gas.).
For limiting reactants you have to actually do the problem 2x. Once assuming one of the reagents is the limiting and again assuming the other is the limitant. The trick is to start with a balanced reaction and to pick one substance and convert everything into that one substance. So for example 2. I would set it up as follows...
1. Balance the reaction
__O2 +__H2 = __H2O
When I do this I get...
1-O2 + 2-H2 = 2-H2O
2. Plug in numbers
___2.41 g O2__(From Question)_|_1 mole O2 (From Reaction)_______ |_2 mole H2O (From Rxn)
| 32.00 g O2 (From Periodic Table) | 2 mole H2
= A moles of Water
___3.67 g H2___|____1 mole H2___ |___2 moles H2O__ = B moles Water
| 2.02 g H2 | 2 mole H2
Compare A and B see which one is smaller. The one that ones out first is the limiting reactant. So if A is smaller than B. Oxygen must run out first and therefore oxygen would be the limiting reactant.
% yield is just how much I got divided by how much I should have got *100 to make it a percent.
Usually they will give you how much you actually got and how much you started with. Use the amount you started with to calculuate how much you should have had if you did it perfectly.
Consider the reaction
C + 2-H2 explodes and makes CH4. I put explodes because it sounded cooler. It doesn't really.
Suppose you started with 3.0 g H and you produced 2.7 grams C what is your % yield.
If I did this perfectly all of H should react to produce CH4. Using a periodic table I find H2 weighs 2.02 g/mole. While CH4 weighs 16.05 g/mole.
___3.0 g H2___|_1 mole H2___ |___1 mole CH4 _|_ 16.05 g____| = 11.9 g CH4
| 2.02 g H2 | 2moles H2 | 1 mole CH4 |
Wait how can my theoretical mass be larger than the mass of hydrogen I started with? I added carbon as well. Oh yea. Though my final mass should never be larger that the sum of both parts I added. Carbon AND Hydrogen. If it is I did something wrong.
So If I did it perfect i should haved produced 11.9 g CH4 I actually produced 2.7g.
%Yield = actual yield / Theoretical Yield or real world/ perfect world
=> (2.7 / 11.9)*100 = 22.9% Yea! My reaction lost 87.1% of the stuff I put into it. Meaning I spilled most of my beaker. If my percent yield is ever greater than 100% I probably did something wrong.
Subscribe to:
Comments (Atom)